XFA/Data Handling Model
Note that the information in this document is still planned, but is not yet implemented.
Introduction
Amanda's data-handling model sits at the core of the application. Its purpose is fairly simple: move data between a backup client and archival storage. However, it is subject to some stringent constraints.
- Tapes are linear-access devices, with optimal block- and file-sizes; performance deteriorates rapidly as parameters diverge from these optima.
- Recovery of single files (or "user objects", as described below) should be relatively quick, and not require reading an entire dumpfile.
- Recovery should be possible with only native tools and the contents of tapes.
- Amanda must be able to recover indexes and all other metadata from the on-tape data alone (a "reindex" operation).
Terminology
Much of this terminology is part of the the Application API; this section briefly summarizes those terms..
- Application
- An Amanda component that interfaces directly with the client data.
- User Object
- The smallest object that can be restored (e.g., a file for GNU Tar).
- Collection
- The smallest amount of data that the application can operate on (e.g., a 512-byte block for GNU Tar).
- Transfer
- A data-movement operation.
- Transfer Element
- A component of a transfer; elements are combined in a kind of pipeline, with each element sending data to the next.
- Filter
- A transfer element which performs some transformation, such as compression or encryption, on the data that passes through it. Filters are described as operating normally when performing a backup, and in reverse on restore. When operating in reverse, a filter transforms data that it produced during normal operation, transforming it back into the original input. For example, an encryption filter encrypts in normal operation, and decrypts in reverse.
- Seekable Filter
- A filter which, when operating in reverse, can produce usable output starting from somewhere other than input byte zero; contrast non-seekable filters.
- Non-seekable Filter
- A filter which, when operating in reverse, must always begin at byte zero of the datastream.
- Catenary Filter
- A filter for which concatenation is distributive over filtering. A filter is catenary if
cat file1 file2 | filter | filter -reverse
produces the same output as
(filter <file1 ; filter <file2) | filter -reverse
Gzip, for example is catenary.
- Bytestream
- A linear sequence of bytes; the data exchanged between transfer elements.
- Input Slice
- The consumption of a range of bytes from a bytestream by a transfer element.
- Output Slice
- The creation of a range of bytes in a bytestream by a transfer element.
Diagrams

A bytestream is represented by a solid horizontal line; output slices made by the transfer element producing the bytestream are indicated with tickmarks above the line, while input slices for the consuming element are delimited with tickmarks below the line.
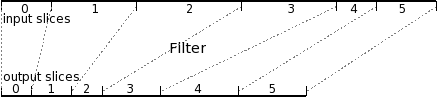
A filter element, then, consumes one bytestream (the upper bytestream) and produces another (the lower). Note that there is a one-to-one correspondence of an element's input slices (against its source bytestream) and output slices (to the bytestream it produces).
A Transfer
Let's look at a full transfer, operating normally:
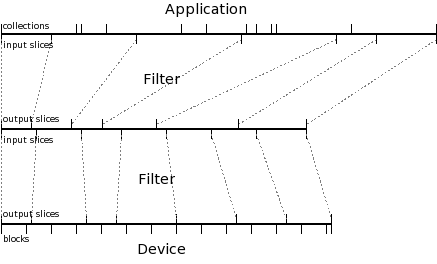
Reading the diagram from top to bottom:
- The application produces a single bytestream, recording (in the index) the byteranges representing each collection.
- The first (topmost) filter divides that bytestream up into input slices, and records the corresponding byteranges in the index.
- The filter produces a different bytestream, containing one output slice for each input slice applied to the first bytestream; the byteranges of the output slices are also recorded in the index.
- The second filter independently divides that bytestream up into input slices, and records the corresponding byteranges in the index.
- The filter produces a final bytestream, containing one output slice for each input slice applied to its source bytestream; it records the corresponding byteranges in the index.
- The destination element divides its bytestream into a number of equal-sized device blocks, and writes it to permanent storage. Note that the final block is shorter than the rest, representing an EOF. See the Device API for details.
The result is the following:
- A mapping of collections to byteranges (from the application)
- For each filter, a mapping of byteranges in the source bytestream to input slices, and output slices to byteranges in the target bytestream
- A mapping of byteranges to tape blocks
- A tape file full of data (possibly split -- we don't address that possibility here)
All of the mappings relate integers (input slices or output slices) to byteranges (represented as an inclusive interval [min, max]). Such a mapping can be stored in an RDBMS efficiently, using O(n) space, where n is the number of input slices or output slices, not the length of the bytestream.
Recovery
Given the above mappings and a tape full of data, we can perform a recovery.
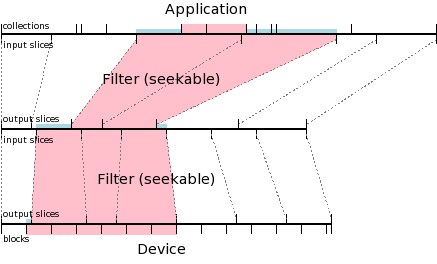
In this diagram, the pink represents the data used for recovery. The blue rectangles are data that are thrown out at each stage of the recovery.
Before the recovery can begin, Amanda does some calculations. Based on the user objects to be recovered, Amanda calculates the collections required; in this diagram, that is collections 4 and 5. Amanda converts these collections into a byterange using the collection -> byterange mapping. Looking at the first filter, Amanda selects the set of input slices that will completely cover that byterange, possibly including some extra data; in this case, input slices 2 and 3 are needed. Amanda converts the equivalent output slices into byteranges in the next bytestream, and repeats the process with the next filter; in this case Amanda needs input slices 1, 2, and 3 from the second filter. Finally, Amanda uses the bytestream -> tape blocks mapping to determine the data blocks that must be read.
Now, working bottom to top, Amanda reads the appropriate blocks from tape, discards a bit of data (blue) to get to the beginning of input slice 1 for the second (bottom) filter, and passes the data to the filter, which operates in reverse. The filter produces another bytestream, from which Amanda must discard some initial and final data, and which is then passed to the first filter. Data in that filter's output is again discarded, leaving only the portions of the bytestream corresponding to collections 4 and 5, which the application uses to recover the requested user objects.
If the required set of collections is not contiguous -- for example, if the user requested one user object near the beginning of the dump and one near the end -- then Amanda has two options. It can restore an entire range of collections including the required collections, and throw out those that are not required; or it can split the recovery into multiple transfers, one transfer for each contiguous set of collections. In practice, the decision of when to split a recovery will be based on heuristics balancing the time required to read some extra collections against the time required to perform multiple transfers.
Complications
Sadly, things are not so simple.
Non-catenary Filters
For all of the filters considered so far -- seekable or non -- Amanda runs a single instance of the filter algorithm to produce the entire dataset. These filters encode enough data into their output that they can "navigate" it when running in reverse, and produce output equivalent to the input data. Unfortunately, many real-life filters do not have this property -- notably most encryption algorithms. These filter algorithms must be restarted for each input/output slice, and as a result the input/output slice boundaries must be known when the filter operates in reverse. This is relatively straightforward during normal operation, as that information is available in the index. However, during re-indexing or native-tools restore, the index is not available.
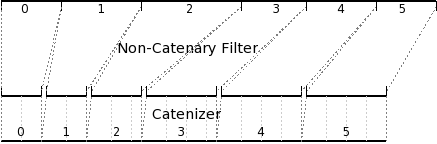
In this diagram, the broken horizontal line in the middle is meant to represent a sequence of distinct bytestreams, one from each run of the filter algorithm. The problem, when operating in reverse without an index, is to know at which byte position to restart the filter algorithm.
Amanda's solution is to encode the length of each output slice in the bytestream, using a "catenizer". Since the length is usually not known until the data is produced, this is done using a blocking operation, with some metadata on each block to indicate whether it begins a new output slice. The details are to be determined, but will probably include some additional metadata and "magic" values to allow the catenizer to recognize and navigate corrupted files.
During normal recovery operations, this technique means that the filter need not consult the index to perform its work, simplifying the system design somewhat. During a reindex operation, the catenizer allows the filter to faithfully reproduce its original input, which is all that is required.
Native-Tools Restores
Native-tools restores, however, are a bit more challenging. The catenizer has produced a bytestream in a "proprietary" format not recognizable to native tools. But without the catenizer, there is no information about byte positions at which to restart the filter. The solution is to write a simple "de-catenizer" in Perl, and include it in the Amanda header along with instructions for its use. That will look something like:
AMANDA: FILE 19780615000001 bkupsvr /var/lib/amanda lev 1 ...
To restore, position tape at start of file and run:
dd if=<tape> bs=32k skip=1 | /bin/gzip -dc | amcatfilter gpg --decrypt | /bin/tar -xpGf - ...
Where 'amcatfilter' is the following Perl script:
#! /usr/bin/perl
...
Non-seekable Filters
Recall that a non-seekable filter is one which cannot begin operation in reverse anywhere but at the beginning of its bytestream. In the recovery diagram above, both filters were seekable, and thus could start at a output slice boundary in their bytestreams. As a result, Amanda did not need to read the beginning of the file from tape, but could jump in at the first block containing data to recover.
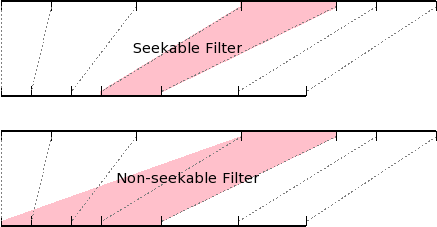
For a non-seekable filter, any input slice corresponds to a output slice which begins at byte zero of its target bytestream. Whereas in a seekable filter, the byteranges for contiguous output slices were contiguous but not overlapping, in a non-seekable filter, all output slices include byte zero. This means that the recovery algorithm specified above works without change, although it must read more data.
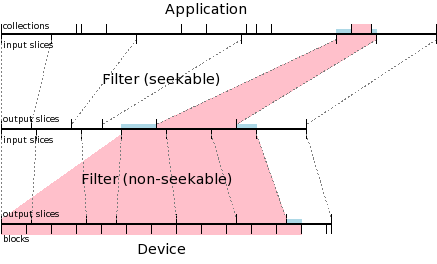
In this diagram, the bottom filter is non-seekable, and thus required that data be read from tape starting at the beginning of the file.
Note that a non-seekable filter can also be made seekable with the catenizing filter described earlier. The decision to apply the catenizer will depend on the startup costs associated with the filter.